生物の体内にはカリウムがあり、その中には一定量の放射性カリウムが含まれていて、これが日常の内部被曝の最大要因になっていると言われています。
「東京もすでに被曝、1平方cmあたり3ベクレル」「東京オワタ\(^o^)/」というようなことがネットで語られているのを以前見まして、ずっと気になっていたのが、「うちのわんこが散歩の時におしっこをすることで、どのくらいの放射性物質を排出してしまっているのか?」という点。
上記のような低濃度の放射能であれば、へたすると、うちのわんこも放出したりしてしまっていないでしょうか。
この点について、ネットを参考に、高校の物理や数学を思い出しつつ計算してみました。
(「竹中平蔵氏の確率計算」の話が話題になってましたが、この「複利の計算」がわかれば、すっきり解決です。)
うちのわんこは 40kgあるのでw、
尿量は人間とほぼ同じと仮定して1日1リットル、小出しに分けるので1回あたり100ccと想定。
犬の尿中に含まれるカリウム量のデータが見当たらなかったのですが、人間は1日あたり1から4グラム程度を排出するとあります。
犬の方が新陳代謝が良さそうなので、多めに見て、我がわんこが1日に尿で排出するカリウムが4グラム、尿1回あたりが0.4グラムと仮定します。
カリウムの原子量は39.0983 g/molなので、0.4gは約0.01モル。
カリウムのうちの放射性のカリウム40の割合は(東京に限らず)0.012%。
1モルの中に含まれる原子の数(アボガドロ定数)は 6.022× 1023。
これらを掛け合わせると、1回の尿中の放射性カリウム原子の数は、約7×1017個と想定できます。
なんと、1兆の70万倍(70京個)もの放射性カリウム原子が、1回のわんこの尿の中に含まれているわけですね。
(追記5/15:すみません、計算が違っていて一桁足りませんでした。結論は変わらず。)
わんこは、とんでもない大量の(原子の個数の)放射性物質をまき散らしているわけであります。
しかし、放射性カリウムは、一瞬にして放射線を出して崩壊するわけではありません。
半減期1.3億年をかけて徐々に半分まで減って行きます。
報道でもよく耳にする 放射能の量「ベクレル(Bq)」という単位は、放射性物質の量そのものではなく、1秒間あたりに原子核が1つ崩壊して放射線を放つ放射能の量です。
つまり、放射性物質が多くても、半減期が長ければ、その分、放射能は小さくなります。
追記11:00:
もちろん、半減期が長い方が放射性物質の減り方は少ないので「放射能は減ります」「小さくなります」という言い方に違和感を感じられる方もいらっしゃるかも知れませんが、放射能とは放射線を出す能力のことなので、放射性物質の原子の数が同じなら、半減期が長い方が放射能は小さくなります。(対時間経過ではなく、対半減期で減少)
ただし、放射「能」ではなく放射性「物質」の減り方は小さくなりますので、少ない放射能が長く続くわけです。
では、半減期1.3億年の放射性物質は、1秒間にどのくらいの割合で崩壊するでしょうか?
ここで、複利計算の(文系的)知識がちょっと役に立ちます。
年利が r で、1年経った後に金利が付く場合には、1年後の元利の合計額は元本の 1+r 倍になります。(単利)
この金利を元本に組み入れて、それにさらに金利が付くのが「複利」です。
半年複利だと1年後の元利合計は (1+(r/2))2、毎月の複利だと(1+(r/12))12、毎日の複利だと(1+(r/365))365、毎秒の複利だと(1+(r/31536000))31536000になります。
こうして金利の元本への組み入れをどんどん細かくしていくと、金利が無限大に膨れ上がっていくような気がするかも知れませんが、実はそれほどは変わりません。
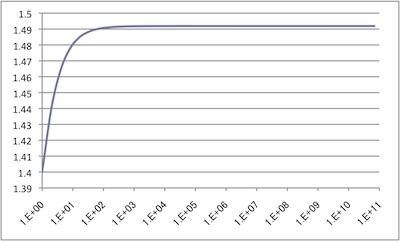
(上図は(今は亡き)年利40.004%のケースで、組み入れ回数nを横軸(対数目盛)にとって (1+(r/n))n を計算したものですが、見てのとおり、組み入れの頻度を10倍から100倍くらいにするともう、それ以上はあまり変わりません。40%が49%になる程度。
「複利は怖い」と思われていますが、経済合理性のある年利で組み入れ頻度を上げるより、絶対的な年利を上げる「トイチ」とかの方がより効くわけです。)
この数式の一般形 (1+(r/n))n の n を無限大に近づける極限(n→∞)を取ると、収束して、元利の合計額は、er (自然対数の底 e の r 乗)になります。
t 期間後の元利合計は、(1+(r/n))nt の極限で er tとなります。
これを放射性物質に応用して考えます。
1秒間あたり放射性物質が減少する割合を b、半減期をT(秒)とすると、半減期を経過した時点の放射性物質の割合は、(1 – (b/n))nT の極限(n→∞)をとって、e-bTとなることがわかります。
半減期というのは量が半分になる期間ですから、e-bT =1/2 となるわけですが、この式を満たす b を求めればいいわけですね。
対数の定義や公式を思い出すと、
loga(ax)=x
loga(b/c)=loga(b) – loga(c)
ですから、
e-bT=1/2
の両辺の対数(eを底とする対数 ln [natural logarithm])を取ると、
ln(e-bT)=ln(1/2)
左辺は何乗の肩の部分が外に出て、右辺は分母の2を分子にもってくるとマイナスが外に出て、
→ -bT = -ln(2)
両辺をマイナスTで割ると、
→ b = ln(2)/T
つまり、この b(2の対数を半減期で割ったもの)を放射性物質の原子の数に掛ければ、1秒間に崩壊する原子の数が計算できることになります。
ln(2)は約0.693
で、カリウム40の半減期は1.3億年(=1.3×109×365日×24時間×60分×60秒 ≒ 4×1016秒)なので、
1回のおしっこの中に含まれる放射性カリウムが1秒間に崩壊する個数は、
1回の尿中の放射性カリウム原子の個数(7×1017個)×ln(2)(0.693)/ 半減期(4×1016秒)=12個
となります。
すなわち1回の尿の放射能の量は12ベクレル(Bq)。
1回のおしっこが10cm四方(100平方cm)に広がるとすると、1平方cmあたり0.12ベクレル。
3匹のわんこが同じところにマーキングしても、だいたい1平方センチあたり0.3ベクレル程度の増加にしかならないはずです。
そもそも人体には、数千ベクレルのカリウムが入ってますし、庭に(カリウム入り)肥料を撒くと、1kgあたり数千ベクレルの放射能で「汚染」されるようですので、それに比べれば、わんこが排出するおしっこは(放射性物質の量に限れば)たいしたことない、と言えそうですね。
(ではまた。)
[PR]
メールマガジン週刊isologue(毎週月曜日発行840円/月):
「note」でのお申し込みはこちらから。








磯崎さん
今回のエントリ、ありがとうございます。
都内ですが、幼ない息子がいるのでいろいろ心配していました。
このような実際の数値を使った説明は、本当、安心感の根拠になり、母親としても、ありがたいです。
あと、(未知のことゆえ)騒ぐ前に、まず理解しなくてはと痛感しました。
また、有用なエントリを期待しておりますね!!
1.3億年->13億年ですね。
1.3×10の9乗の方は正しいようです。
http://cnic.jp/modules/radioactivity/index.php/4.html