昨日のエントリーの続き、です。
（以下、ご自分で解きたい方は、ネタばれにご注意、です。）
第２問
昨日の第一問の答え「7427466391.com」に、アクセスしてみると、以下のような問題が表示されます。。

Congratulations. You’ve made it to level 2. Go to www.Linux.org and enter Bobsyouruncle as the login and the answer to this equation as the password.

f(1)= 7182818284
f(2)= 8182845904
f(3)= 8747135266
f(4)= 7427466391
f(5)= __________

f(5)に入る数字がパスワードになるわけですが、それはなーに？というわけです。
まずは、軽くアタリを付けようと思って、またもやExcelを使用してグラフを書いてみると、以下のような感じ。（これも、渡辺千賀さんのblogにf(5)の解答が載っていたので、それもプロットしちゃってますが。）

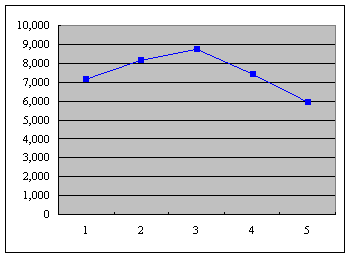
（単位：百万）
うーん。一見、２次曲線ですね。
Excelで上のグラフの青い線を右クリックして「近似曲線の追加(R)…」を選択、対数近似、多項式近似、累乗近似、指数近似等、ぜんぶやってみたけど、当然のように、ぴったりグラフの線に重なることはありません。（そんなに甘くはない。）
で、よーく数値を見返してみると、どれも10桁の整数です。10桁の整数・・・って、第１問の答えも10桁の整数だったと思ってよく見直してみると、f(4)の答えが第１問の答えと同じじゃん！（大ヒント、ですね。）
「ということは・・・」と思って、必殺超最先端テクノロジー「Ctrl+F」を使って、f(1)からF(4)までの値について、昨日の自然対数の底「e」の数列を文字検索してみると・・・・

e =2. 718281828459045235360287471352662497
7572470936999595749669676277240766303535
4759457138217852516642742746639193200305
9921817413596629043572900334295260595630
7381323286279434907632338298807531952510
・・・

・・・・出ました出ました。
これらの数列は、やはり、「e」の数列の中に現れる10桁の連続した数字のようです。
（最後の「5966290435」は、渡辺千賀さんのホームページにあった解答。）
ここからが難問
f(n)の現れるeの小数点以下の桁数をa(n)として表してみると、
a(1)=1
a(2)=5
a(3)=23
a(4)=99
（ついでに、解答の数字は、a(5)=127）
アタリを付けるために、これをまたグラフにしてみると、

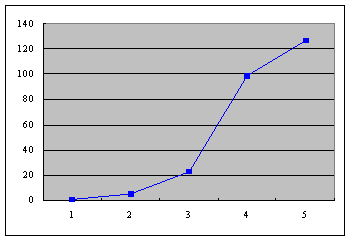
・・・こんな感じです。
eとか素数が好きそうなので、たぶん、その辺の組み合わせなんでしょうけど。
a(4)以外は、全部素数なんですが、a(4)だけ99で素数じゃない。だから、素数の表の中で一定間隔でたどっていく、というような単純なものではない、ということになります。
a(1)=1なので、次の2つの素数2と3を足すと「5」=a(2)、次の3つの素数5、7、11を足すと23=a(3)、といういい感じで進むのですが、次の４つの素数13、17、19、23を足しても72にしかならず、a(4)=99とは合いません。（あれぇ〜？）
（すでに渡辺千賀さんのホームページで答えを見ちゃっているので上のグラフがわかってるわけなので推測できるわけですが）、そもそも解答の「5」のところで数字がサチっちゃってます。単純に素数の順番のかけ算とかで増えていくなら、前の数字との差はどんどん開いていくはず・・・。（うーん。）
ま、この程度の数字遊びで解けたら、それこそ「文系でも解けちゃう」問題になっちゃいますからね。（←負け惜しみ。）
ということで、本日は、ここまで。