イギリスの数学者ハーディが、彼が見つけ出したインドの天才数学者ラマヌジャン（イギリスの風土が体に合わなかったのか入院中）を見舞った時に、

「今、乗ってきたタクシーのナンバーは、1729というつまらない数だった」

というと、ラマヌジャンは、すぐさま、

「それはつまらない数などではなく、正の３乗数の和で２通りに表すことができる最小の自然数です。」

と答えた・・・というのを、先日の「たけしの誰でもピカソ」でやってました。
（ビートたけし氏は、最近、数学にハマってらっしゃるそうです。）
で、問題の1729ですが、
1729＝12³ + 1³ = 10³ + 9³
と、２つの3乗数の和で2通りに表されるのですが、「なんでそんなことが一瞬でわかるんじゃい！」と思いますよね？ 私も、すごい人もいたもんだ、と思ってたんですが、先日、朝目覚めた時に、ぱっとひらめいて、なんとなくラマヌジャンの頭の中が垣間見れたような気がしました。
フェルマー予想
数学者にとっては、x³ + y³という形は非常に馴染み深いものだったはずです。
なぜなら、「3 以上の自然数 n について、xⁿ + yⁿ = zⁿ となる 0 でない自然数 (x, y, z) の組み合わせが存在しない」、というフェルマー予想（フェルマーの最終定理）の証明は、数学者にとっては最大の夢のひとつだったはずなので。
インド人は99×99まで九九を習う？
ほんとかどうか存じませんが、インド人の九九は99×99まであるとか。
1729というと、非常にデカい数のような気がしますが、（99×99の話がホントなら）天才数学者でなく、普通のインド人にとっても、かなり「小さいほう」の数なんじゃないでしょうか。
（追記：いただいたコメントやwebなどを見ると、2桁の九九はかなり一般的だが、99×99まで覚えている人は、かなりマレのようですね。）
実際、20までの3乗数を一覧表にしてみると、下記のとおりですが、

黄色い色をつけたあたりは、実は、インド人じゃないみなさんでも比較的見覚えがある数字じゃないでしょうか。
9の3乗数（81×9）までは、インドの九九のテーブルに(ほぼ)含まれる数字なわけですね。ラマヌジャンだったら、20の3乗数くらいまでは、ぜんぶ「馴染み深い」数字だったんじゃないかと。
と考えると・・
「1729」という数字を見た時に、まず必ずや、「1728（＝12³）と1違いじゃん」というのはラマヌジャンの頭の中に一瞬で思い浮かんだはずです。（この間、0.01秒）
1＝1³というのは日本の小学生でもわかりますから、フェルマー予想に慣れた頭なら、1729＝12³ + 1³という絵はすぐ思い浮かんだはず。
もひとつ、「1729」という数字を見ると、「729」という数字が容易に見てとれます。
729は前記のテーブルのとおり、9の3乗数。1000が10の3乗数だということは、これも日本の小学生でもわかりますので、1729＝10³ + 9³と表せるのは、ラマヌジャンなら、同じく0.01秒で頭の中に浮かんだのではないかと思います。
ラマヌジャンは数学の専門家なので、「つまらない」と言われると「ほんとにつまらないかな？」という職業的猜疑心が働いたはず。この2通りの3乗数で表される数が特別な意味を持つには、あと何の「役」がつけばいいか？
２つの3乗数の和だけなら、9＝1³ + 2³とか、もっと小さい数があるのは自明。（0.01秒）
1729が、他の２つの3乗数の和で表せないのも自明。１と9と10と12を使ってしまっているので、後は11³を使うしかないが、これは当てはまらない。（0.02秒）
とすると、1729が「２つの3乗数の和で表せる最小の数」というのはどうだ？（0.1秒）
・・・というところまでは一瞬で到達したと思うのですが、この先（1729が要件を満たす最小の自然数であることの証明）が、ちょっと凡人では想像が難しくなってきます。
11³が入る1729未満のケースは上記でつぶしたとして、10³＋9³の和より小さい異なる数の3乗数の組み合わせは、下記のとおり、45通りしかありませんので、ラマヌジャンならしらみつぶしでも一瞬で解けたとは思いますが、もうちょっとエレガントなひらめきがあるんでしょうか？

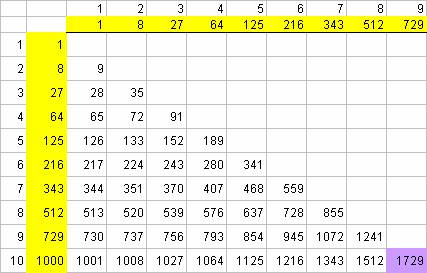
前述のフェルマー予想をn=3で実際に数字を当てはめてみたことがあったとすると、上記のような数字たちは、ラマヌジャンにとっては、すでに「メモリー上に展開されている」ものだったかも知れません。
（後半、エレガントなひらめきが出なかったのが悔しいですが・・・ではまた。）